The Circle of Fifths

The circle of fifths is a way of visualizing the relationship of the twelve notes of the scale and the key signatures of each of the keys major and minor. The circle of fifths is one of the most useful tools for notating, transposing, for understanding key signatures and getting a handle on the structures of music. It’s usually represented as a circle within a circle, the outer circle represents the major scales and chords, and the inner circle represents the minor scales and chords.

The simplest key, of course is C major, only white keys on the piano, no sharps or flats. Now we haven't talked about modes. For now it's enough just to understand that what we recognize as a major scale is a scheme of half-steps and whole-steps that determine the intervals between the notes. Do-re-mi-fa-so-la-ti-do sounds natural and familiar to us.

But this familiar major scale is just one of many possible schemes of intervals. This scheme of whole steps and half steps is called the Ionian mode. There are six other common modes as well as some variants. You can demonstrate most of them just by starting on different notes of the white keys. For now, let's just assume we're talking about the C scale, only white keys and the chords built on the notes of that C major scale.

Chords, as we have discussed, are usually three notes, called a triad, and those three notes are the 1st, the 3rd and the 5th notes of the scale. So a C major chord would be C, E, and G. If we start on the A or the sixth note up the scale, then we would have A, C and E. This chord will sound very different because it is a minor chord. What determines whether a chord is major or minor is whether that third note is found by moving up four adjacent keys (four half-steps) for a major third, or up three adjacent keys for the minor third. The half-steps are called semitones.

Using only the white keys, we can see that from C to E is a move up four adjacent keys, and from A to C only three adjacent keys. So the minor third is a smaller interval and has a more melancholy sound than the bright, positive sounding major third. Much more to discuss on this topic, but for now let's focus on the relationship of chords to keys and how to account for their sharps and flats.

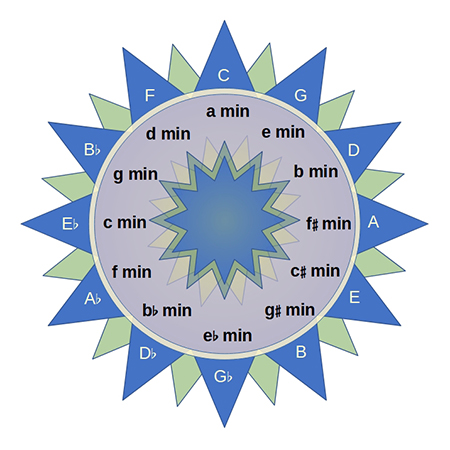
As we look at the circle of fifths we can see that the next key in the circle as we move clockwise, is G. G is the fifth note on the C scale. Now here we're not talking about adjacent keys, we're talking about the notes of the scale. We call this the V chord since it is the built on the fifth scale degree.

We also say that G is the dominant chord of the key of C. That is a way of saying that the G chord is the countervailing harmonic statement that offsets, or calls for resolution to the C chord. You can try playing the G and the C chord alternately a few times to see how this relationship works. There is a sort of 'shave and a haircut, two bits' thing happening as we go from the G to the C on 'two bits.' Play a few of your favorite songs in C and notice how the G chord is used to set up the ending or resolution, the run from third base to home.

If we are playing a song in G then we find that we need to enlist another chord to give us that same sense of resolution, and that turns out the be a D major chord. Now we have left the familiar neighborhood of C and the safety of the white keys, and we are confronted with our first sharp. As we move around the circle of fifths, we pick up a sharp for each step we make to the right.

If we start on G on the white keys only and play them in order, before we can finish the scale we encounter something strange. As we get up close to completing the scale, we strike the F which doesn't sound as we expected, and doesn't seem to offer the chance to land on the G in a satisfying way. We find that we have to move to the next adjacent key, the F♯ in order to have that desired sense of 'ti do' or 'shave and a haircut, two bits' resolution. So we have our first sharp, and sure enough, when we play the D chord, the dominant chord for the key of G, there it is, our first sharp, the F♯. Play these chords a few times on the guitar or keyboard just to get it all straight in your mind and in your ear.

So you can see that as we move to the next position on the Circle, we will encounter the key of D. Again, as we play the notes of the D scale on the white keys of the piano, we'll have to incorporate the F♯ in order to make the third note of our scale sound right, and we'll have to raise the seventh note as we did before from C to C♯ in order to satisfy that musical longing.

You can see that as we move around the circle, we are adding a sharp for each new key. So we can say that D is the key with two sharps. I remember some of the bar bands I played in would use hand signals to call out the key of a song, two fingers meant the key of D. It also could mean send over another beer for me and the bass player.

Now every key has a related minor scale which we call its 'relative minor.' This scale is demonstrated by playing the notes of the scale starting on the sixth scale degree. So in the key of C, the relative minor scale would start on the A. You will notice that the chord which is created when we use the first, third and fifth scale degree of this a-minor scale is an a-minor chord. Again, this is because the third is a minor third, or three adjacent keys from the tonic note, the A. Give some thought to this.

We use an upper case letter to designate a major chord, and a lower case letter for a minor chord. This can be helpful when we use the shorthand of Roman numerals to designate a chord progression such as I vi IV V I, (tonic, relative minor, subdominant, dominant and tonic,) a very familiar series of ‘changes.’ A-minor is so often used in songs in the key of C, and it and the dominant chord (G) and the sub-dominant chord (F), can all be created with just the white keys of the piano.

There is one exception to this. When we play the dominant chord, and set up the tension that 'wants' to be resolved to the tonic or home chord, we often use a form of the chord that has one more note in it. That note is the seventh scale degree, but a minor seventh, or flat seventh. So the G7 chord would have the F natural in it instead of the F♯. This seems odd, but sounds right.

My sense of this is that we need to set up an attractive dissonance, that is, that the F 'wants' to resolve down to the E note in the C chord as the B in the G chord resolves upward to give us that 'ti do' ending as it moves to home base. Again playing these chords back and forth a few times will settle this in your mind in a good way. Also it's good to notice that the D and the F in the G7 chord provide a nice harmony as they move down in tandem to the C and the E of the C chord. We call this parallel harmony, or parallel thirds.

One other thing to note, is that when you have the G chord resolving to the C tonic chord, one dissonance that also ‘wants’ to be resolved is the tension between the B and the F of the G7 chord. This interval is controversial in addition to being dissonant. It is what is called a ‘tritone.’ because it is made up of three adjacent whole tones or six semitones.

It is a half-step smaller than the ‘perfect’ fifth of seven semitones that we need in a major or minor triad so it’s called a ‘diminished fifth’ or an ‘augmented fourth.’ Over the centuries there has been a lot of controversy about this interval. It has been known as the ‘devil’s interval’ or ‘diabolus in musica.’ It does seem to insist on being put to rest by resolving to the tonic chord.

Next on the circle is the key of A. Again, by playing the notes of the D scale we'll encounter that same issue with the seventh scale degree, and predictably we'll have to raise it a half-step to sound right. So the C has to become a C♯. This continues to be true as we move around the circle all the way up to seven sharps in the key of C♯ and that makes sense, since by now every note has had to be raised that remedial half-step.

If we go back to the C at the top of the circle, and move in a counter-clockwise direction, we encounter the same issue, but this time it is resolved by adding a flat, by moving the fourth scale degree down by a half-step. This might seem counter-intuitive since it was the seventh scale degree that was the problem with each successive move to the right. But if we start on the D scale and move back to the G scale, we can see that it's the seventh scale degree of the key of D, that has to be moved down a half step (C♯ to C the fourth scale degree of the key of G) to get us back to the relationships of intervals that our ear wants to hear in G. Think about it for a minute and it will make sense.

And, as we did on the clockwise side of the circle, moving to the left presents us with the need to flatten the fourth scale degree of each key as we move around the circle. Again, the key signature for F will have one flat, the B♭, and then the key signature for B♭ will have two flats as we change the fourth scale degree, the E to E♭. Confusing, but starting to make sense?

A glance at the circle shows that as we move clockwise from key to key, each subsequent key will incorporate the sharped note of all the keys before it on the circle, except for the one right before it. So the A will have a key signature with a sharp on the F, the C and the G lines of the staff but not the D.

On the counter-clockwise side, each subsequent key adds a flat named for the adjacent key after it. This can seem confusing, but in pondering it we may discover more confirmation of some of the properties of the circle. It's not exactly an object of mysterious powers, but maybe close to it. Maybe a Rosetta Stone, or kind of a circular Ouija board of musical composition.

When we have completed the circle, we can see that some of the keys overlap. F♯ can be expressed as the key with six sharps, but it will sound exactly the same as G♭, the key with six flats. Strange to think that the key of F♯ has a natural F note in it, but then the seventh scale degree of a major scale is going to be the note which is a half-step lower than the tonic note. This can lead to some strange anomalies like the occasional double-flat, but let's just try to keep it between the ditches.

Now, when we think of using the circle of fifths as a tool of composition that's when the fun begins. You will notice that the top quarter of the circle contains the C, F, and G major chords, but it also contains the d, a and e minor chords. We can play most popular songs from the last few decades with these six chords alone. The fun really starts when we venture into the territories of related keys and their chords, unexplored territories for the most part, at least in our experience up to now.

There is an additional chord in each key, which does not have a home in the circle of fifths for reasons of simplicity, but it can be a very useful, if complicated, harmonic element. The seventh chord of the key of C is B-diminished. It's called diminished because the minor third from the one to the three (B to D), which is three half-steps, is joined by a minor third from the three to the five (D to F), another three half-steps, making only six half-steps from the root to the fifth, creating what's called a diminished fifth.

Normally a chord, either major or minor, will have what's called a 'perfect fifth’ an interval of seven half-steps or semitones. The third can be major (four half-steps) or minor (three half-steps) but then the complimentary interval from the three to the five will always compensate by being either three half-steps or four half-steps to make the fifth a perfect fifth.

In the case of a diminished chord the stacking two minor thirds creates an unstable and provocative sounding chord. This chord can be very useful and we will get to some of the ways it is used, but it's definitely an outlier as far as the normal key chords are concerned. You'll find a diminished chord in the Beatles' song, "When I'm Sixty-Four" and "Michelle" and in the bridge of the Eagles' song, "Heartache Tonight."

Any quarter of the circle of fifths will show the six related chords of the key which is chosen, leaving out the one diminished chord for each key. One very productive step in the search for interesting substitutions or alternate chord ideas is to explore the parallel minor key. While the relative minor key to C is a-minor, the parallel minor key would be c-minor. And just as the scale of a-minor is based on the C scale, the scale of c-minor is based on the E♭ scale. Strange, but logical, and musically pretty exciting.

It’s quite a step into new territory for the song, but very promising for the songwriter. The key of E♭ brings you the major chords of E♭, B♭ and A♭, and the minor chords of c-minor, g-minor and f-minor. Lots of useful and intriguing harmonic possibilities to work with.

Like the color wheel, with its complimentary colors at opposite or triangular locations, the circle of fifths offers lots of hints as to what might be pleasing combinations of hues and tones.

By associating the chord that is central to the key with its dominant and sub-dominant on either shoulder, you have a whole harmony scheme at any place around the wheel you may find yourself. But then there are also interesting excursions into other relationships of chords and scales. Also when you open the door to not only the minor chords based on the tonic key but those based on related keys as well, the possibilities for color and emotional richness are increased for your songwriting.

Songs that consciously employ more adventurous elements of the circle seem to have a wonderful sense of moving forward, of traveling into harmonious regions on the way to a satisfying resolution when the home base is reached with the tonic chord. C so often goes to F and then back to C, or on to G and then back to C, but many writers have kicked down the traces and gone from C to A to D to G and back to C; or from C to F to E7 to A7 to D7 and to G7 and back to C. Aside from just traveling around the wheel, much can be gained by choosing an element from an unexpected place, and the circle can give you the tools to navigate the unknown regions. Your ears will be your guide.

Songs that employ interesting elements from the circle of fifths are:

“Sweet Georgia Brown”

Louie Armstrong and his band are featured in this video. The lead clarinet is by Joe Darrensburg.

My dad and I attended a jam session of the Southern California Hot Jazz Society in Burbank many years ago and Joe Darrensburg played piano. I remember my dad commenting that he wished he knew more about the voicings of chords that Joe was playing.

This is a pretty amazing version from Django Reinhardt and Stephan Grapelli

Tony Sheridan and The Beatles with Pete Best and Stuart Sutcliffe performing “Sweet Georgia Brown:”

“Nobody Knows You When You're Down and Out”

Eric Clapton does a great version of the song, always one of my favorites to sing.

“Pachelbel's Canon”

Here’s a nice explanation of the theory elements of the Canon from Allysia van Betuw.

“Something In the Way She Moves”

Here’s a discussion by Jake Lizzio of George Harrison’s song “Something”. He goes into considerable depth, and I encourage you to stay with it and even watch and play along with it more than once if this is new to you.

If you play the song in C there is a nice easy walk from C major to C major7 to C7 and then F. In the next section, he goes to a D7, this chord is a borrowed dominant leading us to G and then to the a-minor for kind of a surprise, almost a false ending, but then the a-minor with the G♯ as again, we walk by half steps to the a-minor7, and then the D9, the next step in the half-step walk down. This is serious hit record songwriting. Some of these ideas are just a close step into innovation, and some are bold steps.

Again, the circle of fifths can help you navigate into unknown territory, and again, you ears will confirm your experimentation (or not). Jake likes to talk about the modes in explaining how he understands unexpected chords, and that’s something worthy of another article. It’s enough just to get a whiff of that aspect of things. He goes on to show some possible substitutions and offer his theories about them. It’s the kind of exploration that will give us some new song ideas.

Jake has done a series of tutorials under the heading ‘Perfect Progressions” and number 4 is devoted to a similar discussion of John Lennon’s song “Imagine”. These are very informative lessons.

Here’s a keyboard to help you visualize some of these ideas.